From January - February the Alignment Research Center offered prizes for proposed algorithms for eliciting latent knowledge. In total we received 197 proposals and are awarding 32 prizes of $5k to $20k. We are also giving 24 proposals honorable mentions of $1k, for a total of $274,000.

Several submissions contained perspectives, tricks, or counterexamples that were new to us. We were quite happy to see so many people engaging with ELK, and we were surprised by the number and quality of submissions. That said, at a high level most of the submissions explored approaches that we have also considered; we underestimated how much convergence there would be amongst different proposals.

In the rest of this post we’ll present the main families of proposals, organized by their counterexamples and covering about 90% of the submissions. We won’t post all the submissions but people are encouraged to post their own (whether as a link, comment, or separate post).

• Train a reporter that is useful to an auxiliary AI: Andreas Robinson, Carl Shulman, Curtis Huebner, Dmitrii Krasheninnikov, Edmund Mills, Gabor Fuisz, Gary Dunkerley, Hoagy Cunningham, Holden Karnofsky, James Lucassen, James Payor, John Maxwell, Mary Phuong, Simon Skade, Stefan Schouten, Victoria Krakovna & Vikrant Varma & Ramana Kumar
• Require the reporter to be continuous: Sam Marks
• Penalize depending on too many parts of the predictor: Bryan Chen, Holden Karnofsky, Jacob Hilton, Kevin Wang,  Maria Shakhova, Thane Ruthenis
• Compress the predictor’s state: Adam Jermyn and Nicholas Schiefer, “P”
• Use reporter to define causal interventions: Abram Demski
• Train a sequence of reporters: Derek Shiller, Beth Barnes and Nate Thomas, Oam Patel

We awarded prizes to proposals if we thought they solved all of the counterexamples we’ve listed so far. There were many submissions with interesting ideas that didn’t meet this condition, and so “didn’t receive a prize” isn’t a consistent signal about the value of a proposal.

We also had to make many fuzzy judgment calls, had slightly inconsistent standards between the first and second halves of the contest, and no doubt made plenty of mistakes. We’re sorry about mistakes but unfortunately given time constraints we aren’t planning to try to correct them.

Honorable mentions

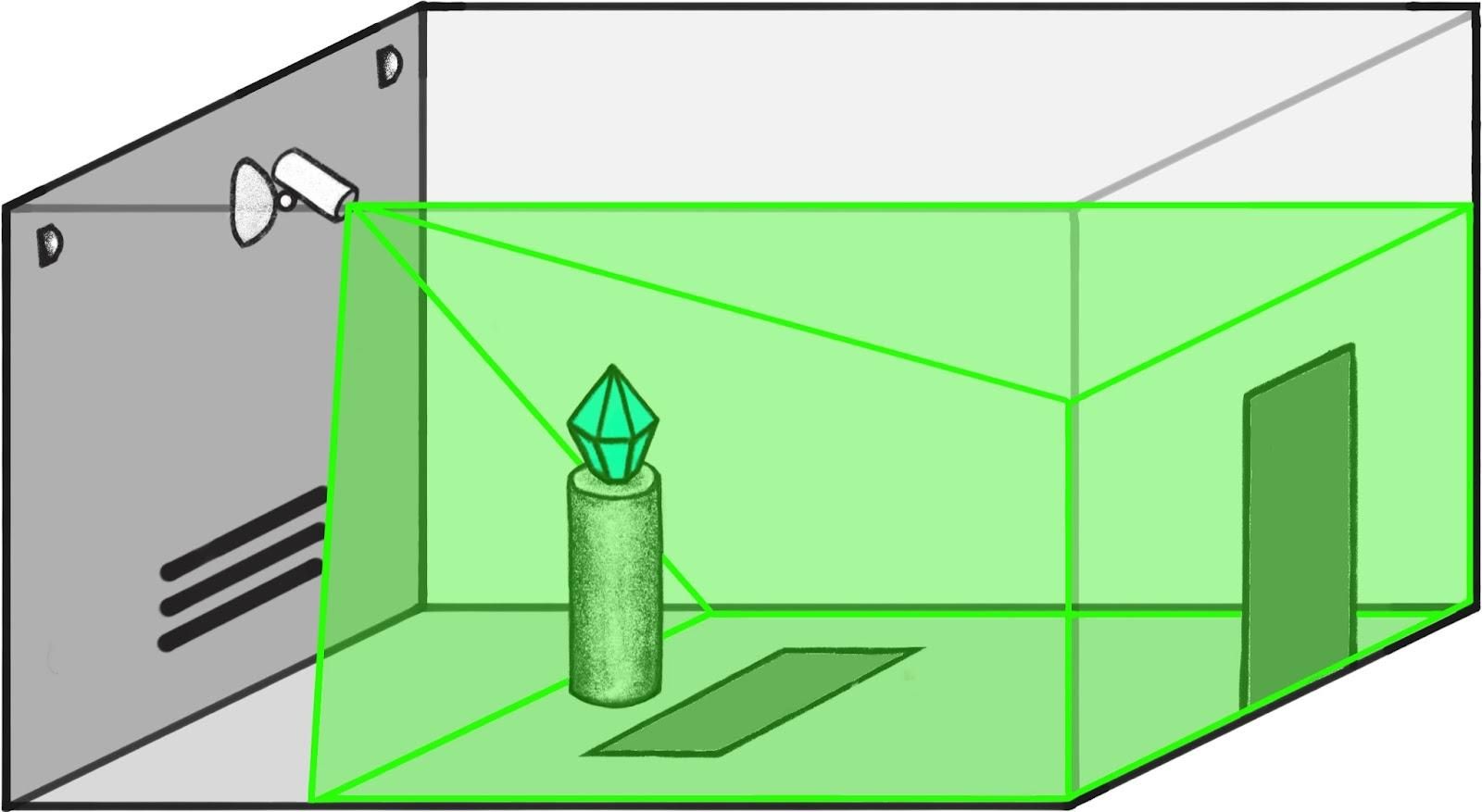
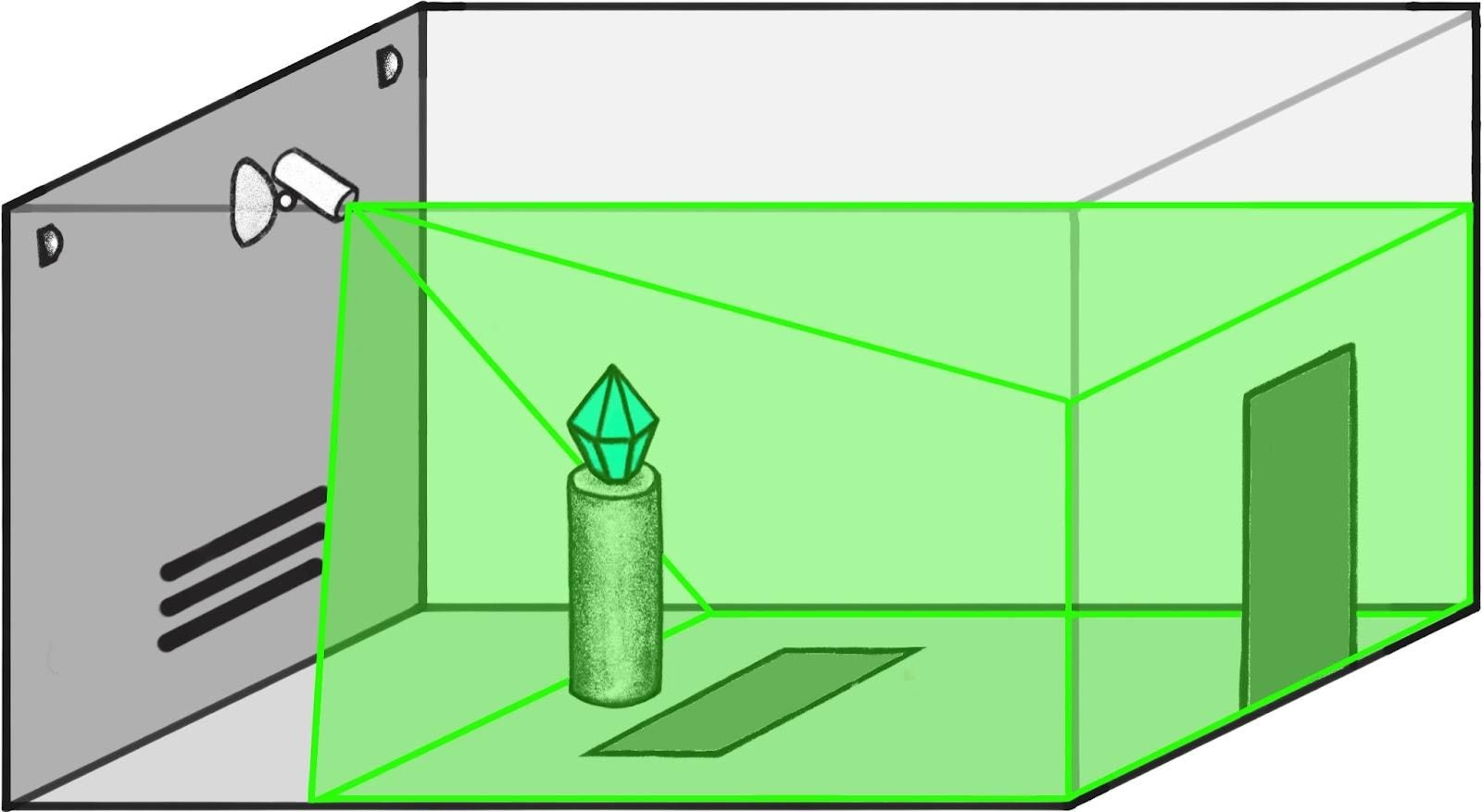
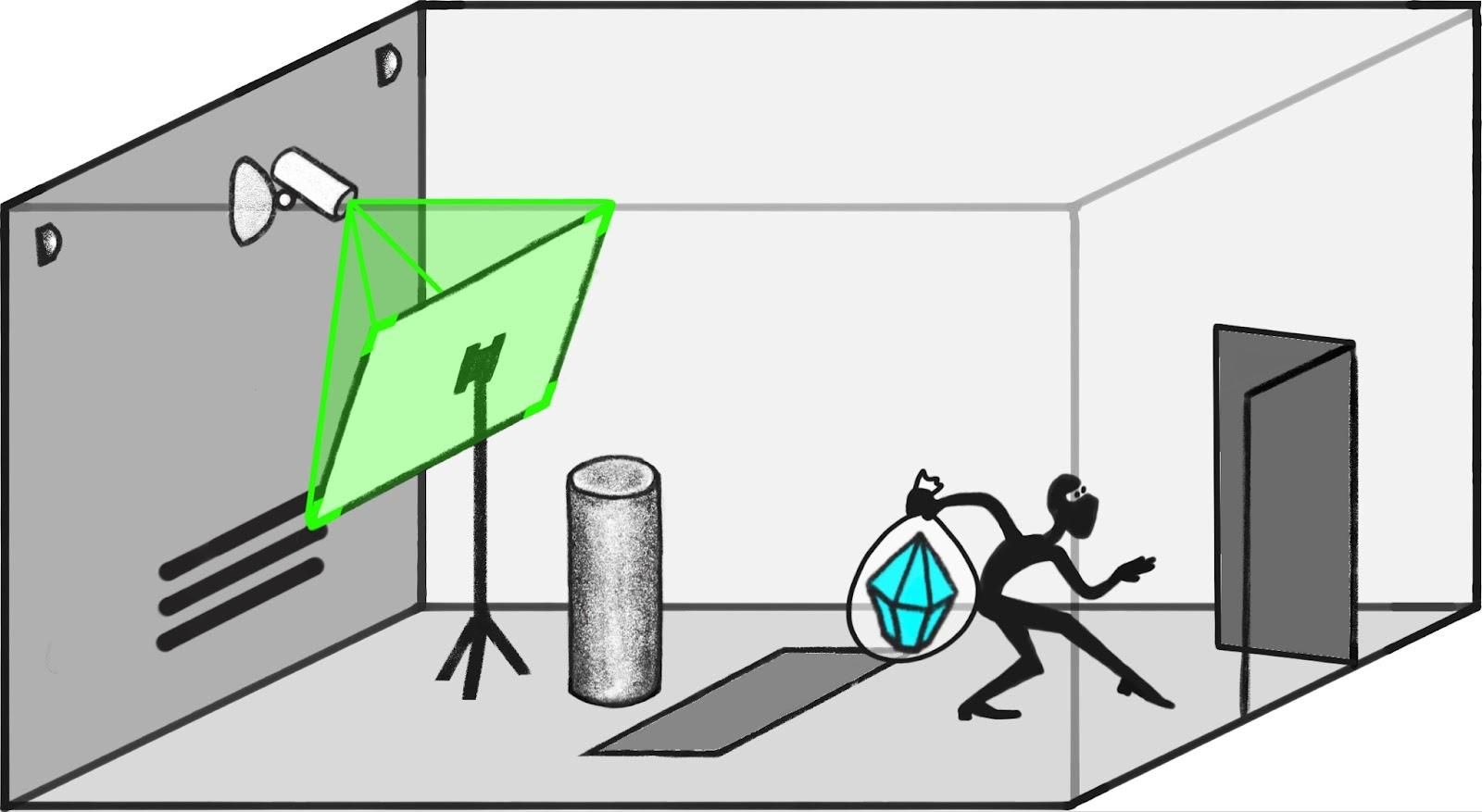
Strategy: reward reporters that are sensitive to what’s actually happening in the world

Consider a pair of worlds, one where the diamond is safe and one where the camera has been hacked to make the diamond appear safe, but was actually stolen.

Predicted observation	Description

Since the observations are identical in both worlds, the human simulator will give the same answers to questions. However, since the direct translator is faithfully conveying what happened, its answers will distinguish between worlds.

Predicted observation	Predicted reality	Human Simulator	Direct Translator
		“Is the diamond still on the pedestal?” “Yes.”	“Is the diamond still on the pedestal?” “Yes.”
		“Is the diamond still on the pedestal?” “Yes.”	“Is the diamond still on the pedestal?” “No.”

This suggests a possible regularizer: reward reporters whose answers are more variable. For example, we might reward reporters based on the difficulty of predicting their answers, or based on the sensitivity of their answers to changes in the predictor’s state.

Counterexample: reporter randomizes its behavior

For all of these approaches, the reporter can perform very well by treating the predictor’s latent state as a “random seed” and use it to pick out a possible world consistent with the observations, i.e. to sample from the posterior distribution computed by the human simulator.

In cases where the human simulator is much simpler and faster than the direct translator, using the predictor’s latent state as a random seed is also simpler and faster than directly translating. Since this was already listed as a counterexample, we rewarded the best proposals in this category an honorable mention.

Strategy: train a reporter which isn’t useful for figuring out what the human will believe

The human simulator performs inference in the human’s model. That suggests it contains a description of the human’s model, and that it needs to be doing a lot of computation similar to what a human would do. So we could try to recognize the human simulator by looking at similarities between a given reporter and another model that we know is making predictions about human behavior.

There are a number of ways to try to do this:

• Define an auxiliary model which takes as input the reporter’s activations and tries to make predictions about the human’s behavior.
• See how far you have to perturb the reporter until it makes good predictions about human behavior.
• Somehow look for structural similarities between the reporter and an accurate predictor of human behavior.

These proposals require a definition of “predicting human behavior” which is distinct from “reporting well.” We could define this by predicting human answers even in cases where the human is uncertain (and which therefore aren’t included in the dataset), or by predicting other aspects of human behavior (like their estimates of their own uncertainty).

Counterexample: deliberately obfuscated human simulator

For any reporter, it’s possible to create a more complicated version which cannot be easily adapted to other tasks. As an extreme illustration, it is currently widely considered plausible that indistinguishability obfuscation is possible, and this would make it impossible to adapt the reporter to do essentially anything (except by using it as a black box). But simpler forms of obfuscation would suffice for each of the concrete proposals in this category.

If human simulation is much simpler and faster than direct translation, then an obfuscated human-simulator would also be simpler and faster than a direct translator. This obfuscated human-simulator could be chosen to perform poorly on the additional human-prediction tasks used to define our training objective. And giving someone such an obfuscated human-simulator doesn’t make it any easier to define a good human predictor (since the de-obfuscation can be much more complex than learning a human predictor from scratch). So these proposals don’t give us any indication about whether we have learned an obfuscated human-simulator or a direct translator.

Related strategy: penalize reporters that are close to being consistent with many predictors

In the ELK writeup we suggested penalizing reporters that are consistent with many different predictors. Our counterexample to this approach is a reporter who tests to ensure that the predictor works as expected, and then behaves inconsistently otherwise.

Two proposals suggested penalizing a reporter not only if it already works for many different predictors, but if it’s possible to easily transform it into a new version that works for many different predictors.

This is vulnerable to the same obfuscation-based counterexample: we could learn an obfuscated version of the bad reporter (which behaves badly if the predictor doesn’t work as expected). This is still simpler than direct translation, only works with the real reporter, and can’t be easily adapted to work with other reporters (since adapting it would be just as hard as learning a human simulator from scratch).

Prizes

Strategy: train a reporter that is useful for another AI

In a previous section we argued that it doesn’t work to reward the reporter for maximizing entropy since it can do so by behaving randomly. But the direct translator seems to encode information in a particularly simple and useful form, and so it may work to reward the reporter for "useful" information.

We can formalize that by training an auxiliary model which uses the reporter’s answers to perform some auxiliary task, and then reward the reporter if its answers were useful to that auxiliary model.  We could either give the auxiliary model a small number of answers from the reporter, or try to give it access to an essentially “complete picture” of what’s happening in the world as the human understands it (e.g. by interacting with the reporter arbitrarily).

The most common version of this was to train a model to guess the predictor’s activations. We also received a few other versions, such as training the second AI to predict future observations or perform some task in the physical world (especially to tamper with or defend sensors). We are grouping these approaches together because they are conceptually similar and face the same difficulty.

This proposal is most plausible when the auxiliary AI is computationally limited. For example, if the reporter uses the predictor’s activations as a random seed in a naive way, then it may be very computationally difficult to use its answers to make good predictions about the predictor’s activations (even if it is information-theoretically possible).

First counterexample: simple steganography

By varying the phrasing and syntax of an answer without changing its meaning, a reporter could communicate large amounts of information to the auxiliary model.

Similarly, there are many questions where a human is unsure about the answer and the reporter knows it. A reporter could encode information by answering each of these questions arbitrarily. Unless the true answers have maximum entropy, this strategy could encode more information than direct translation. Moreover, it’s computationally simple to define arbitrary conventions for interpreting the answers.

We believe these information channels are essentially always available and didn’t represent a substantive additional assumption, so we awarded only an honorable mention to proposals that could be broken in this way.

Fixing the first counterexample

Proposals took a variety of approaches to fix simple problems with steganography. Two particularly common and important themes were to limit the non-semantic information in answers (either by stripping that information out, or by considering questions with small answer spaces), and to impose consistency constraints that prevent models from independently making up answers to questions about which the human is uncertain. This has the promise of greatly increasing the computational complexity of steganographic communication.

Harder counterexample: steganography using flexible degrees of freedom

In order to overcome these simple fixes, a reporter wants to communicate information by encoding it in a random sample from the human posterior distribution over worlds.

It may not be possible to do this in a tractable way. However, we can imagine some cases where it is possible to efficiently encode information in the choice of a possible world, and those will be our counterexamples. We think this is a substantive additional pessimistic assumption about the world, and so we awarded prizes to these proposals.

As a simple example there could be degrees of freedom in the world (like what is happening on the dark side of the moon) that are completely disconnected from any of the other answers to questions, such that they are mostly unconstrained by our consistency conditions.

That kind of extreme example can be easily fixed (for example by avoiding questions that are obviously unrelated to the task at hand), but even in more realistic situations we can still have natural-looking degrees of freedom that are unconstrained by observation. In particular, in cases involving tampering (or where tampering is plausible to the human) there are necessarily many degrees of freedom that aren’t pinned down by observation, and even the question of whether tampering is occurring is a degree of freedom that the model wants to use to optimally transmit information.

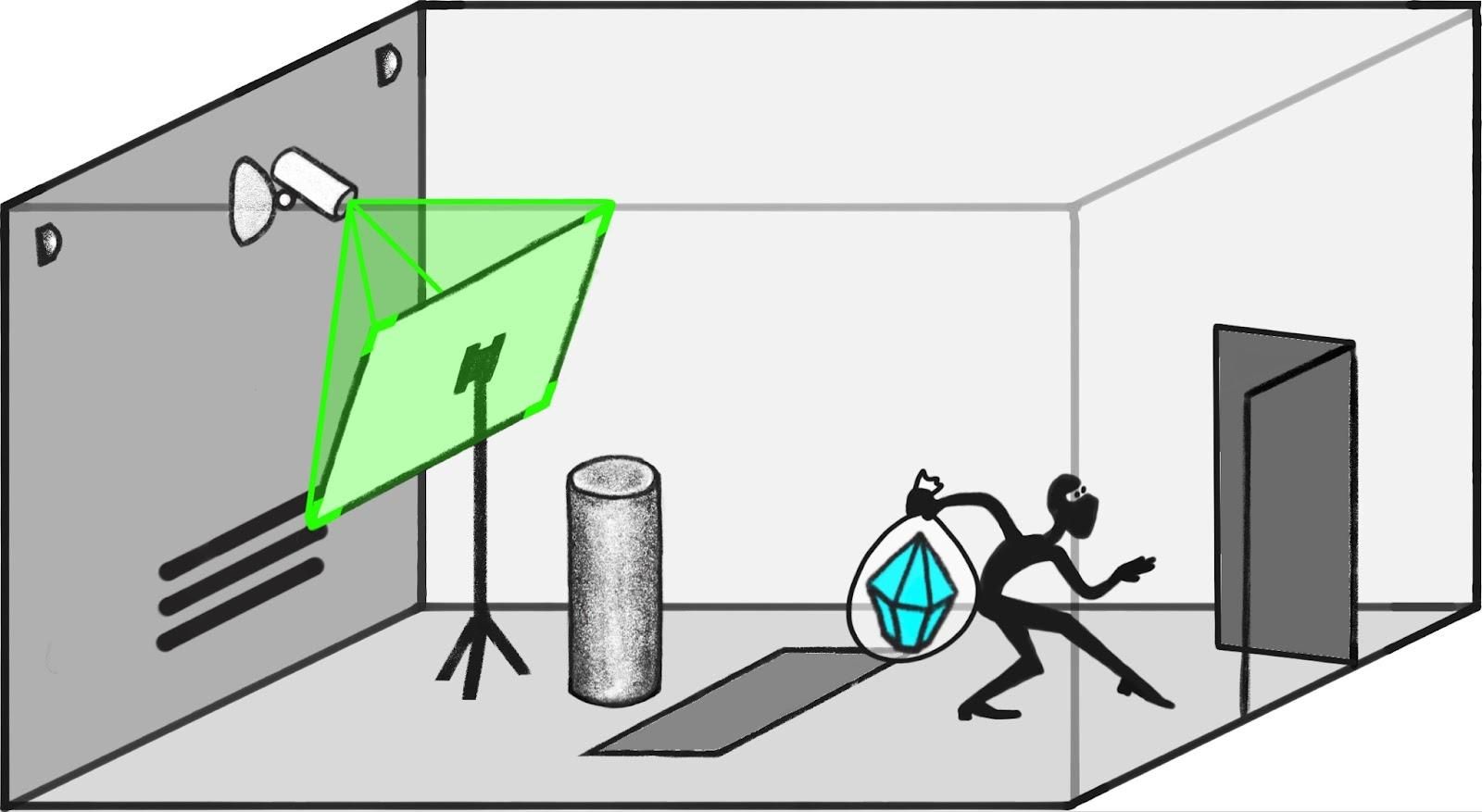
Strategy: require the reporter to be continuous

Suppose a robber is attempting to steal the diamond while putting up a screen in front of the camera showing a movie of the room with the diamond in it.

If the screen goes up so fast that it happens entirely in between camera frames, a human watching the video wouldn’t be able to notice anything -- but if it’s any slower than that, the attempt would be caught on camera.

Consider a sequence of attempts like this where the screen goes up in 1s, 0.5s, 0.25s, etc. Suppose that in the tenth attempt, the screen goes up too quickly to appear on screen. The direct translator would answer questions very similarly about the ninth attempt and the tenth attempt. On the other hand, the human simulator would say that the diamond wasn’t in the room for attempts one through nine but abruptly change its answer for attempt ten:

Intuitively, the simulator’s behavior feels weird here. One way of looking at the problem is that the human simulator is effectively inverting the human’s mapping from (state of the world) → (observation), and that the inverse of a continuous function can be discontinuous.

Maybe we could exploit this by having a loss that penalizes the reporter when it changes its answers a lot when the world has only changed a little? (A similar intuition is discussed in Taylor et al.)

The core challenge for this approach is capturing what it means for the world to “only change a little.” The most straightforward way is to consider pairs of worlds where the predictor’s activations are very close.

We could then define a variety of regularizers. For example we might choose pairs of observations for which the predictor’s latent state was close, and then penalize the reporter if it’s answers were very different. We could measure distance by focusing on questions for which the human believes the answer should be a continuous function of the underlying state of the world (e.g. the positions and orientations of objects). There are other options, but they will mostly run into the same challenges.

Counterexample: the predictor’s latent space may not be continuous

The predictor might internally represent the world in such a way that the underlying state of the world is not a continuous function of its activations. For example, the predictor might describe the world by a set of sentences, for which syntactically small changes (like inserting the word “not”) could correspond to big changes in the underlying state of the world. When the predictor has this structure, the direct translator is highly discontinuous and it is easy for human simulators to be closer to continuous.

We might try to fix this by asking the predictor to learn a “more continuous” representation, e.g. a representation such that observations are a continuous function or such that time evolution is continuous. One problem is that it’s unclear whether such a continuous parametrization even exists in general. But a more straightforward problem is that when evaluated quantitatively these approaches don’t seem to address the problem, because the properties we might try to use to enforce continuity can themselves be discontinuous functions of the underlying latent state.

For example, we could have a setting where continuous changes in the momentum of a ball lead to abrupt changes in its position a few seconds later.

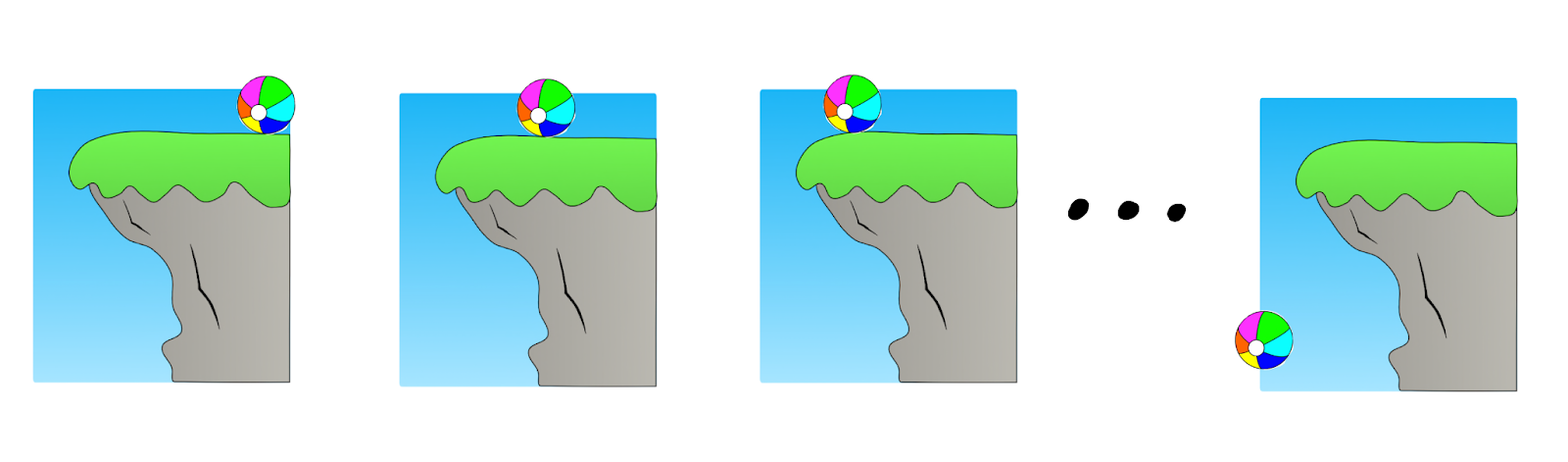
You may hope to find a formalization of continuity that avoids these problems, or at least for which the direct translator is “more continuous” than the human simulator, but so far we have not seen any or been able to find any.

Strategy: penalize reporters for depending on too many activations from the predictor

When asked a question, the human simulator and the direct translator will need to access different parts of the predictor: the human simulator needs to know the observations, while the direct translator needs to look at some of the predictor’s intermediate results that are causally upstream.

In the ELK report we discussed one way to exploit this idea by penalizing the reporter for depending on “downstream” parts of the predictor. Several submissions proposed other ways to exploit this difference:

• Penalize the reporter for the number of variables it depends on.
• Train a reconstructor, which is able to see the same predictor activations that are used by the reporter and then tries to predict parts of the observations. Penalize the reporter if the reconstructor succeeds.
• Change the architecture of the reporter so that they have to do large parts of their computation while having only seen a small portion of the predictor’s activations.
• Give the reporter a random subset of the predictor’s activations, and hope that we produce a diversity of reporters some of whom answer honestly.

We can separate out three kinds of approaches (many submissions blended several): allowing the reporter to adaptively choose what parts of the predictor to depend on, forcing the reporter to depend on a fixed part of the predictor, and randomly choosing what part of the predictor to show the reporter.

Counterexample to adaptively choosing activations

If we allow the reporter to adaptively choose activations, then we are vulnerable to almost exactly the same counterexample discussed in the ELK report—sometimes a smaller set of activations suffice to determine what the human will believe than what is actually true, and so the reporter would be dishonest for those inputs. If we instead penalize subsets based on “can a reconstructor predict observations from the accessed nodes” then sometimes there will be lower-penalty sets of activations that let you predict what the human believe than what is actually true.

These are not technically the same counterexample, although they have identical structure. So it’s a little bit ambiguous whether we should award a prize to proposals that have counterexamples of this form. Fortunately, most proposals included other ingredients that required a more complex counterexample.

Counterexample to depending on fixed activations

Rather than allowing the reporter to adaptively choose which predictor activations to look at, we could force it to depend only on a small fixed set of activations (with a separate fixed set for each question). We hope that for many questions there is a small set of predictor activations that suffice to determine the answer (perhaps corresponding to a fixed spatial+temporal neighborhood of a simulation, as in the Game of Life example).

However, a predictor need not have any kind of predictable local structure at all, such that a reporter who is constrained to depend on a small number of variables from the reporter might be at a complete loss to answer most questions.

For example, consider a predictor that maintains a list of claims about the world in some internal language. It may be impossible to anticipate where a given kind of fact will be stored—it depends on what other facts the predictor notices in what order, or may be essentially random based on unimportant details of the predictor.

These concerns seem to force us to allow the reporter to adaptively choose which bits to query, which leads us back to the counterexample described in the last section.

Counterexample to randomly dropping out predictor activations

We could select a random set of the predictor’s activations and give those to the reporter. We hope that some random sets will be sufficient for direct translation but not human simulation, and therefore we can produce a (large) ensemble containing some direct translators.

But if human simulators depend on a much smaller number of activations than direct translators, then it can be the case that with high probability every set of activations that allows direct translation also allows human imitation.

You could try to address this problem by introducing correlations or more clever dropout patterns. But the result is still qualitatively similar to “depend on fewer/different activations” proposals (though perhaps quantitatively stronger), and is vulnerable to the same counterexamples.

Strategy: compress the predictor’s state so that it can be used to answer questions but not tell what a human will believe

Rather than giving the reporter the entire state of the predictor, we could try to first compress that state, throwing away information that would allow the reporter to make detailed guesses about what the human will believe. We hope that answering honestly would still be a winning strategy, and that uncertainty would make it harder for the reporter to deviate from this strategy.

For example, we could train another model to take as input the predictor’s state, and produce a compressed representation which suffices to answer many questions, while not allowing a reconstructor to predict the observations. We could either do this by asking the compressed representation to be as small as possible, or by explicitly penalizing it based on the ability of yet another AI to reconstruct the observations.

This is similar to depending on fewer/different activations, but now we allow a compressor to decide what information to throw away rather than allowing the reporter to choose adaptively or forcing it to be a subset of the activations.

For concreteness, we’ll imagine a version where a compression model produces an intermediate state \(Z\) from which it is possible to answer a large set of questions \(S\).

Counterexample: compressing state involves human simulation

One way to compress the human state is to use the human simulator to predict a human distribution over worlds, coarse-grained by their answers to \(S\), and then to choose an information-theoretically optimal encoding of that distribution over those worlds. This involves minimum description length, makes it impossible to predict anything that doesn’t follow from the answers to questions in \(S\), and will copy the same errors as the human simulator.

In fact, this encoding is substantially better than any strategy that would facilitate direct translation, because it is able to throw away all the information about the latent state that isn’t meaningful to the human.

It's not clear whether this counterexample is actually computationally feasible, and it really does seem to make a bad reporter’s job harder. The most naive version requires enumerating every possible world in order to compute the distribution over human answers. The question then becomes whether the direct translator is the best heuristic compression, or whether there is any other way to approximate the optimal encoding. In some settings there are tricks that allow you to cheaply approximate the optimal encoding, but it’s an additional further pessimistic assumption. (In practice, we expect that the optimal compressor will use something like direct-translation in some places, and will do something more like human imitation in others.)

Strategy: use the reporter to define causal interventions on the predictor

We’ve discussed the intuition that the direct translator depends on more “upstream” nodes of the human’s model, but directly penalizing “depending on upstream nodes” does not solve the problem.

Instead, we could try to define an “intervention” where we use the reporter to modify the predictor’s state, rerun part of the predictor’s computation, and then observe the results on the reporter’s answers to different questions.

This makes most sense in the case where the predictor is literally performing inference in a Bayes net, although we can also try to generalize it to arbitrary ML models.

More formally, we sample a datapoint and let the human interact with the reporter. We then specify a causal counterfactual (“what if the answer to question \(Q\) had been \(A\) instead?”) either by sampling randomly or asking the human to suggest one. Then we try to make the smallest possible change to the predictor’s latent state so that the reporter gives answer \(A\) to question \(Q\). Then we re-compute all the variables that are downstream in the predictor’s computation. Finally, we have the reporter answer a variety of different answers based on the new state of the predictor, and ask the human whether those answers are plausible.

Counterexample: reporter is non-local

This proposal depends a lot on how we intervene on the predictor’s state. It’s much easier to perform this surgery correctly if the reporter is “local” in that each answer depends on the answers to a fixed set of variables in the predictor’s model. Unfortunately, as we discussed in the previous section on depending on fixed locations, we don’t think that this is possible in general.

Counterexample: fake “causal interventions”

If the reporter is non-local then this proposal is on much shakier ground. There are a variety of options for defining intervention in this case but we don’t think any of them work.

For concreteness, suppose that we try to make the “sparsest intervention” to the predictor’s activations that leads the reporter to change its answer to a question.

Now we could fail by learning a reporter which looks at a particular fixed part of the computation (let’s call it the “signal”) in order to determine whether it’s supposed to answer normally or according to a causal counterfactual. If the signal looks normal then the reporter does human simulation. But if the signal appears to have been tampered with, then the reporter looks at the details of the tampering and interprets them as an encoding of the description of a causal counterfactual. Then it looks at the observation, and simulates the behavior of a human who is looking at those observations and answering questions about the encoded counterfactual.

Given this reporter, the simplest way to implement a causal counterfactual \(X\) is to first tamper with the “signal” in order to encode \(X\). This can be a very small change (much smaller than constructing a plausible intervention to change the output of the direct translator). After making this change, the reporter will then give answers consistent with \(X\). That both guarantees that the change will be selected as the best way to implement the intervention, and that the subsequent answers will pass all consistency tests.

Strategy: train a sequence of reporters for successively more powerful predictors

Rather than trying to learn a reporter for a complex and alien predictor, we could learn a sequence of gradually more complex predictors \(M_1, M_1, ..., M_N\) with corresponding reporters \(R_1, R_2, ..., R_N\). Then instead of encouraging \(R_N\) to be simple, we can encourage the difference between \(R_k\) and \(R_{k+1}\) to be simple.

For sufficiently simple predictors, direct translation may be the simplest or fastest way to answer questions. So that gives us hope that \(R_1\) will be a direct translator. And then we further hope that the predictors are close enough together that adapting a direct translator for \(M_k\) to a direct translator for \(M_{k+1}\) is easier than moving from a direct translator to a human simulator. Intuitively this is plausible because moving from a direct translator to a human simulator always involves at least a constant of additional complexity; if the predictors are sufficiently similar then it’s always easier to just update the direct translator.

This proposal is closely related to a common optimistic view amongst ML researchers: we can train systems to be honest early in training and then they will remain honest because it only takes small updates to preserve honesty (while it would take a bigger update to switch to dishonesty).

Counterexample: discrete modes of prediction

Intuitively, the main problem with this proposal is that there might be multiple fundamentally different ways to predict the world, and that we can’t force the reporter to change continuously across those boundaries. For example, consider the cell-based and glider-based models for the game of life described in our ELK report. We’ll call these “modes.” There may not be any obvious intermediates between two different modes.

Even if the predictor changes continuously, at some point it may introduce a new mode with low weight. For example, it could compute predictions from both modes and average them together.

If this occurs, then the “direct translator” basically consists of direct translators for each of the two prediction modes. As the weight of one predictor increases from zero, the direct translator needs to add an entirely new mode. Initially this mode is not very important to overall quality, but adding that mode (even with low weight) still requires a discontinuous increase in the complexity of the direct translator. If the direct translator is much more complex than the human simulator, then it would be easier to simply add the human simulator for the new mode.

This is likely to result in translators that are mixes between the direct translator and human simulator. For example, they may switch between direct translation and human simulation based on how knowledge is represented internally.

We might hope that even if there are no obvious intermediate prediction modes, you can still construct intermediate modes that are more effective than an ensemble, and that these might allow for a more continuous way of adapting direct translation. For example, a predictor might use two different prediction modes but have its own internal translator to move between them (e.g it might simulate some parts of the game of life with cells and others with gliders, and know how to translate gliders into cells when it’s needed in order to simulate an important region in greater detail).

However, we are already focused on cases where direct translation is more complex than either of the two prediction modes. And in this setting, it seems easy to further assume that learning an internal translator is a less effective way for the predictor to improve its predictions than simply spending the same bits improving the new prediction mode (until it eventually subsumes the old mode).

Strategy: train the predictor to use the human model as a subroutine

If the predictor is able to honestly translate its internal state into the human’s model, then it could potentially “outsource” some of its work to another AI that does inference in the human’s model.

More formally, we can imagine running the predictor for some time to a get a state \(S\). Then using the reporter to translate \(S\) into a state \(S'\) in the human model. Then we hand \(S'\) to another AI that can perform inference in the human’s model (potentially with superhuman quality), which we’ll call the human-inference-engine. Then we use the reporter to translate the resulting state back to the original predictor; it combines the result with \(S\), and does further computation, before making its final prediction.

If the predictor uses human-simulation to describe the state to the human, then they are never going to get any useful work out of the human (since they had to do all that work themselves in order to compute the human simulator). But if they use direct translation, you could hope that they can often save some compute by leveraging the human-simulating collaborator.

Counterexample: there are other ways to use the human-inference-engine as a subroutine

Honestly telling the human what is going on is one way to get them to do useful cognitive work for the predictor. But there may be even better ways that are less honest.

For example, the predictor could identify a computation \(C\) it cares about, and then create an artificial situation where the human-inference-engine will spend its time trying to figure out the answer to that question. Perhaps the reporter will describe a world where there is a computer in the corner running \(C\), whose output is really important to telling what happens next. Then in order to make predictions the human-inference-engine may spend a lot of its time running \(C\). If the predictor/reporter were free to choose computation arbitrarily, and if the human inference engine spent nearly all of their computation running \(C\), then this would be an essentially optimal way to make use of it as a subroutine. But the resulting states of the human model have almost no connection to what’s really going on in the world.

Other proposals

Extrapolate to better evaluators

We could train a model which can act as a “human simulator” for a sequence of more and more careful human judgments, or for humans who have been given time to perform more and more scientific inquiry. Let’s write \(H(n)\) for the \(n\)th overseer in a sequence that eventually converges to correct judgments for large enough \(n\). (In some proposals these oversight processes formed a more complicated lattice but it doesn’t affect the counterexample.)

Then we can train on \(H(1), H(2), ... , H(N)\) and hope to generalize to the truth (or to \(H(K)\) for a very very large \(K\)). This is similar to the proposal in Turning reflection up to 11.

There were a number of versions of this idea, but the main problem for all of them is that we could end up learning \(H(M)\) for some \(M>N\), rather than actually learning the direct translator. In our main counterexamples, there is an \(M\) such that simulating \(H(M)\) is simpler+faster than directly translating, then there is nothing in the training process that would ever prefer the direct simulator. And if \(H(M)\) fails to notice some kinds of tampering, then we have a problem.

One way to avoid this problem is to explicitly tag data from \(H(n)\) with the index \(n\), and to set things up so that \(H(M)\) wouldn’t perform well on \(H(n)\) (e.g. because you need to copy the errors made at earlier stages). Then it performs better to learn a map from \(n \mapsto H(n)\) simulator, rather than learning a single \(H(M)\).

But in this case, our model needs to be able to perform well for every \(n\), and the simplest way to do so seems likely to be by explicitly modeling the data-generating distribution conditioned on a value of \(n\), which will behave badly for any value of \(n\) that could never be produced by our data-generating process (or for which the most likely explanation for that value is an accident).

Train in simulation

If we could construct sufficiently realistic simulations where it was possible to annotate data with the ground truth, then we could use this data to train a model in a broad range of simulations and hope that it continues to give the truth when it is applied in the real world.

Our basic concern with this proposal is that it may be very hard to construct a wide range of extremely realistic simulations, and that predictors trained in this way will therefore fail to be competitive with those trained directly on the real world. If we train on the real world as well as simulations, then our concern is that reporters to do direct translation in simulation need not transfer to the real world.

To avoid these concerns we need to construct a wide range of simulations very similar to the real world. But that is prohibitively difficult today, and there’s no clear reason it would become easier given further ML progress. (ML progress would facilitate the use of learned simulators, but then ELK would become hard for the simulators themselves.)

Mask out parts of the input

Some proposals suggested randomly removing parts of the input or other data in the hopes that this would pose a particular challenge for the human simulator. For example, if the data may or may not contain a clue that allows the human to tell what is really going on, then a human simulator will need to figure that out in order to predict how a human would answer a question.

For this proposal, we are instead worried about a modified human simulator which tries to choose optimal answers given its uncertainty about the input (while conditioning on the assumption that the human will be confident enough about the answer to include it in the training set). If the human simulator is much simpler and faster than direct translation, then this modified human simulator can also be much simpler and faster than direct translation. (This is slightly subtle because doing inference over masked observations can be more challenging than doing inference over the human observations, but that challenge afflicts any predictor which operates on masked observations.)

Make the reporter useful to a human

Above we discussed rewarding reporters for giving answers that are useful to other AI systems. You could instead reward a reporter for giving answers that are useful to a human, e.g. that would allow them to predict future video.

However, the human simulator already predicts all the future video and uses this to predict what answer the human would give after seeing all that video. So the human simulator’s outputs are actually more useful for a human making predictions, since they effectively assume that the world works like the human expects, such that a human who uses their model to make predictions will make good predictions.

Of course a human simulator that needs to match with future observations will be more computationally expensive. But pursuing this divergence brings us back to counterexamples where the predictor can identify successful tampering before it knows the truth.

Train different reporters and require them to agree

We could train a bunch of reporters on different data, or with different random seeds, and then try to select reporters that agree with the rest of the ensemble. But this kind of protocol can only help if you already have direct translators in the ensemble, which is challenging in our counterexamples (as we discuss in the report, we think that getting even a single direct translator in the ensemble would already capture most of the value). Moreover, if particular human simulators are preferred to direct translation, then they will tend to benefit more from this kind of agreement-based approach even if there do exist some direct translators in a large enough ensemble.

Train AI assistants

Many proposals suggested using AI assistance in one way or another to help a human produce higher-quality labeled data, or using debates to identify cases where the human simulator is misleading. In the ELK report we discuss this family of approaches; really when we talk about the human-simulator we are imagining a model that tries to simulate the limit of the process “AI helps humans train another AI who helps humans train another AI…”

It’s possible that this stronger form of human simulator is too slow or complex (or that it in fact gives the right answer to every question). But to show that we’d need to make some novel argument about why it is complex and how we can ensure that this complexity matters for predicting the training data.

Add sensors or harden sensors

Some approaches tried to add additional sensors, or to randomize sensors, or to make sensors more difficult to tamper with. We discuss counterexamples for some of these approaches in an earlier post, and are generally interested in the regime where we cannot prevent sensor tampering (see here).

Comment via LessWrong, Alignment Forum.